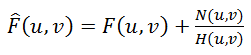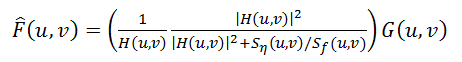本文介绍如何将模糊图片变清楚的相关算法原理。因水平有限,文中出现错误在所难免,希望留言指出。
作为图像处理的子领域,模糊图像恢复是一个很有意思但也非常有挑战性的研究方向。不论是从理论还是实践中,都是如此。比如下面这些场景:
- 照片洗出来后,发现对焦不准,细节看不清楚
- 按快门时,相机有抖滑,拍出的照片有运动模糊
都将是本文要讨论的范围。在此文中,我们不讨论如何修正其它常规图像问题(如:噪点,曝光不足,过曝,形变扭曲)。因为市面上已经有很多工具用来纠正它们。大家多半也都会用这些工具。
为什么目前还没有工具发明出来,以专门用来处理模糊图像呢(锐化不算)?是不是因为无法做到?其实不然,在理论上这其实是可行的。远在计算机发明之前,关于去模糊的数学理论就已经被提出了。不过当时针对是电路信号中的“模糊”问题。此外,就像其它学科一样,算法从提出到实际应用需要相当长的一段时间。
下图展示了模糊图片处理恢复后的效果:
模糊图像数学模型
现在开始从数学角度谈模糊。考虑一张单色灰度图像(彩色图像可以看成由三张R,G,B通道的灰度图叠加),我们定义:
- f(x, y) – 原始图像 (非模糊的)
- h(x, y) – 模糊函数
- n(x, y) – 额外噪点
- g(x, y) – 模糊后的图像
各种情况下,模糊图像的产生过程可以写成如下形式:
g(x, y) = h(x, y) * f(x, y) + n(x, y)
相应的,图像恢复本质上就是寻找一个f'(x, y), 并使f'(x, y)尽可能的符合原始图像f(x, y)。更进一步的看,公式中f(x, y), n(x, y), g(x, y)的含义都是很容易理解的,但h(x, y)就并非那么直观了。以相机模糊为例,原始图像上的每个点都被镜头散射到底片的一小片区域,不再是一个点了。可以想像出,底片上的一个点,都将由邻近区域的点叠加而成的。由于互相重叠,我们看到的图像就被“模糊”了。术语PSF(Point Spread Function, 有时也叫kernel)用来描述单个像素点被模糊后在底片上的图像形状。
PSF (Point Spread Function)
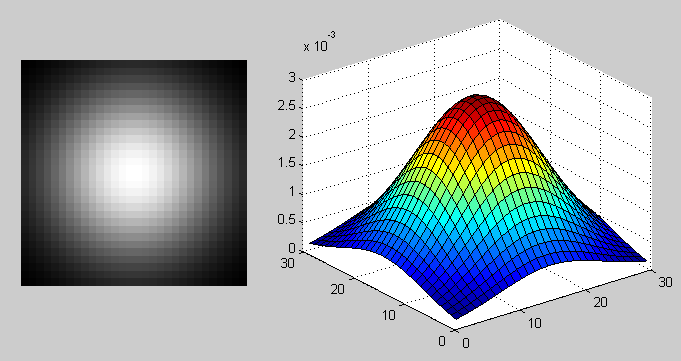
来看一个PSF的实例:
这是高斯模糊函数的PSF: Matlab fspecial(‘gaussian’, 30, 8)
额外说明一下,高斯函数有一个很重要的属性:高斯函数经过傅立叶变换后,依旧是个高斯函数。这让它比较容易作数学变换处理。某些转换操作中的计算损失比较小。
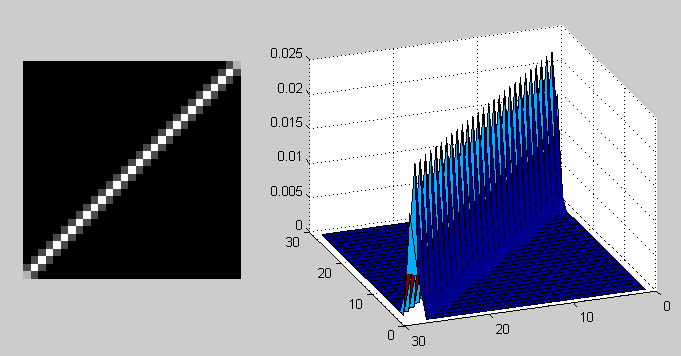
动态模糊的PSF: Matlab fspecial(‘motion’, 40, 45)
将针对单个像素点的PSF应用到整张图像上的数学过程叫:卷积(convoluion). 数学符号通常写做* (注意:和乘法写法相同,但不要搞混)。 从数学上看,对长宽为(M,N)的图像f而言,经PSF模糊函数h后,生成的卷积结果为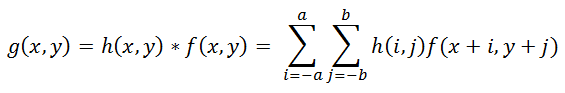
其中,a = (M-1)/2, b = (N-1)/2。卷积的逆过程叫去卷积。去卷积很不常用,数学上用的很少。
卷积计算
卷积计算是很极其消耗CPU的。即使针对现代电脑而言,计算负担也重的无法接受。因此有必要使用一种数学工具用来快速计算卷积。离散傅立叶变换就是这个工具。离散傅立叶变换可将二维图像转成傅立叶空间中的图像,二维中的卷积转成傅立叶空间中的普通乘法。
可以看出,我们先前提到的模糊卷积过程可以写成
后面,我们在傅立叶空间中继续讨论模糊恢复。
去卷积的尝试
之前说过,卷积的逆过程叫去卷积。那么也许我们可以这样用除法计算,来得到恢复后的图像 F^(u, v)
除法是乘法的简单逆运算,但是它恐怕不能像我们预想的那样产生效果。为了理解这个问题,让我们观察方程底部的H(u, v)。如果H(u,v)的值很接近零或者等于零(实际中是必然的),除法将产生一个巨大的无效数值。这个数值将淹没掉正常图像像素值。
以这张图像为例,
转成灰度图,并转入到傅立叶空间后图像如下
左边的是振幅图,右边的是相位图。这里就不详细介绍傅立叶变换了。大家需要知道的知识是,振幅图中数值落差巨大,从图像中心到四个角,数值从百万数量级很快就降至零位。因此,当图像中还含有噪点N(u,v)时,经普通除法运算,这些噪点也会被成百万倍的放大。比如:
噪点比例=0.0000001 噪点比例=0.000005
结论是,如果用除法来做去卷积运算,只要混入一点点噪音,处理结果就被噪声全淹没了。
成熟的去卷积算法
1942年,维纳(Wiener)提出了以他命名的维纳去卷积。这个算法一开始是被设计用来恢复模拟电路信号,稍转变后,其同样适用于图像处理。
式中Sn / Sf也可写做一个常数K, 可近似认为是信噪比。从式中可看出,即使H(u,v)逼近零,结果也不会变得无穷大。除维纳去卷积外,还有其它方法可以用。这里不一一介绍,有兴趣的朋友可以看这本书:<<反卷积和信号复原>>
还有一个更常用的方法叫Richardson-Lucy (简称RL方法)。这个方法是由两位分别独门提出的,所以命名看起来怪怪的。这个方法的思路是迭代计算。

u(t)为期望的原始图像,d是模糊图像,p是PSF, ^p是PSF旋转180度。每迭代计算一次,u(t)就更清晰了一点。不过这个方法也有以下问题:
- 迭代不收敛. 必须要在适合的时候停止迭代,不然继续迭代下去没有用处
- 对噪音有放大作用
目前,实际广泛使用的一般是基于RL的改进版本。
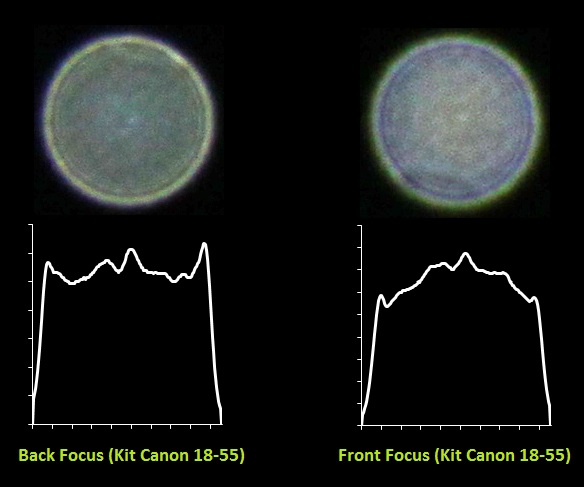
这类去卷积方法需要提供PSF函数。也就是说,你需要知道详细的模糊参数。而这通常是很困难的。比如,从下面两个实际镜头的模糊PSF函数就可以看出, PSF函数是非常不规则的。
基本上,我们只有做实验才能提供出精细PSF函数曲线。这类实验,也只被用于大型设备调教镜头成像细节(如医学CT)。再讲个小故事。当年,哈勃望远镜发射至太空轨道后,大家发现:哎呀,照出来的星系咋这么模糊呢。一调查,发现造主镜的工厂没考虑到地球引力对镜片的弯曲作曲。结果,到了太空后,没有地球引力,镜片微微翘起了一根头发的1/50的距离。但这足以让对焦不准了。咋办呀,大家赶快算理论做实验,很快把这个模糊的PSF函数给搞出来,于是处理一下,效果也还行。当然,哈勃那帮人钱多的是,不满足于软件修复,根据PSF又反造了一块补偿镜放主镜前面。(你要是搞天文摄影的,也可以算算自己的爱机镜头的PSF,咱最起码可以用软件补偿呗。在星图全黑背景上,一颗亮星的成像可以看作镜头的PSF.)。
哈勃补偿前与补偿后成像效果比较。右图是哈勃PSF函数。
盲去卷积 (Blind Deconvolution )
对我们普通人,根本不可能去自己构造PSF函数,比较实用的方法就是让程序自己搜索PSF。这种方法叫盲去卷积(Blind Deconvolution)
2014/6/7更新 (其余待续…)
转帖请注明来自色彩笔
(部分文字图片翻译自smartdeblur)